Alles over Skew-T: de hele atmosfeer in één diagram

Regelmatig laten we bij een onweersverwaching een diagram langskomen dat we ook wel Skew-T-diagram noemen. Het is een uiterst complex diagram met veel lijntjes in verschillende kleuren, maten en richtingen. Soms staat er ook meer informatie bij in de vorm van pijlen en tekst.

Het gevolg is dat heel veel mensen geen flauw idee hebben hoe ze zo’n Skew-T-diagram moeten lezen en wat het nut er überhaupt van is 🙂

En dat begrijp ik volkomen, want het heeft mij ook een behoorlijke tijd gekost om het diagram ‘door’ te krijgen. Het goede nieuws: als het kwartje eenmaal gevallen is, dan vergeet je het ook niet meer.

Wat is een Skew-T-diagram? Wat betekenen alle lijntjes en andere tekens? Waar kun je het voor gebruiken? Al die vragen ga ik proberen in dit artikel te beantwoorden. Heb je nog een andere vraag? Schroom dan niet om helemaal onderaan je reactie achter te laten. We vullen dit artikel graag aan zodat het dient als complete referentiegids voor de meteorologisch geïnteresseerde! 🙂

Metingen met een weerballon

Voordat we het Skew-T diagram kunnen uitleggen moeten we kijken naar een stukje geschiedenis van het meten van het weer.

En die geschiedenis begint natuurlijk aan de grond, bij het meten van allerlei zaken zoals temperatuur, luchtdruk, wind en regen. Daar werden weerstations op land en weerschepen op zee voor gebruikt. De schepen zijn voor een groot deel verdwenen, maar de landstations bestaan nog.

In de Twintigste Eeuw nam de ontwikkeling van de meteorologie zelf ook een enorme vlucht. Door de hoeveelheid metingen konden wetenschappers patronen ontdekken in het weer. Die patronen leidden tot nieuwe onderzoeksvragen en zo was het cirkeltje compleet.

Wetenschappers realiseerden zich echter al gauw dat veel van de patronen niet konden worden verklaard zonder te weten wat het weer is op wat grotere hoogte. Vanaf de jaren ’20 werden er daarom sporadisch door ‘vliegeniers’ metingen verricht. Deze luchtvaartpioniers bereikten natuurlijk ook geen grote hoogtes – de vliegtuigen konden dat immers niet aan. Wél kon de meteorologie zich verder ontwikkelen, maar het was nog niet genoeg.

Sinds dat moment werden er met enige regelmaat weerballonnen de atmosfeer in gelaten. Deze ballonnen worden ook wel radiosonde genoemd. Ze worden bevestigd onder een ballon die gevuld is met helium die vervolgens de lucht in wordt gelaten.

De vlucht van de weerballon duurt vervolgens één tot twee uur. Wat er wordt gemeten? Temperatuur, luchtvochtigheid en luchtdruk, op alle hoogtes waar de ballon vliegt. De radiosonde bevat een locatiebepaling zodat de ballon kan worden gevolgd. Op basis daarvan worden windsnelheid en -richting berekend.

Het KNMI, ons eigen weerinstituut, begon in 1947 met het oplaten van weerballons. Dat gebeurde toen nog twee keer per dag.

Inmiddels wordt er nog maar één keer per etmaal een weerballon opgelaten. Dat gebeurt om 0.00 uur UTC-tijd (1.00 Nederlandse tijd of 2.00 uur Nederlandse tijd afhankelijk van winter- en zomertijd).

Intekenen op de kaart: het Skew-T diagram

Goed – de weerballon meet dus het weer in een groot deel van de onderste atmosfeer (tot-ie uit elkaar klapt). Dat betekent meestal dat er metingen tot 25 kilometer hoogte beschikbaar komen.

Maar ja, zo’n enorme bak gegevens – wat doe je daarmee?

Heel vroeger gebruikten weerkundigen daarvoor een emagram. Dat is een zogeheten ’thermodynamisch diagram’ dat de stand van zaken in de atmosfeer kan weergeven, op verschillende hoogtes. Maar dankzij de ontwikkelingen in de meteorologie was zo’n emagram niet meer geschikt. In 1947 werd er dan ook een voorstel gedaan om een aantal zaken te veranderen. Dat werd door veel mensen binnen de meteorologische ‘community’ overgenomen. Het Skew-T log-P diagram, kortaf het ‘Skew-T diagram’, was geboren.

Als er metingen op worden getekend heet het diagram ook wel sounding.

En het ziet er zo uit – zonder dat er metingen op zijn getekend:

Afbeelding door Paulschou, in het publieke domein beschikbaar.

Naast metingen ook verwachtingen: de progtemps

We kennen echter ook zoiets als een weersverwachting. Op het nieuws zien we meestal een weerkaartje met daarop voor een aantal plaatsen zonnetjes en wolkjes ingetekend, aangevuld met temperaturen.

Maar wist je dat er een enorme bak gegevens schuilgaat achter deze weersverwachting?

Allereerst worden er verschillende weermodellen gebruikt die gemiddeld vier keer per dag een nieuwe weersverwachting berekenen. Dat doen ze in stappen van drie tot zes uur vooruit (afhankelijk van het weermodel) en kunnen meestal 4 tot 14 dagen vooruit kijken (ook afhankelijk van het weermodel).

Ze berekenen de weersverwachting voor ‘vakjes’ van X bij X kilometer, waarbij X soms 1 kilometer is, soms 20 kilometer.

En om het nog maar wat complexer te maken: ze kunnen feitelijk de hele atmosfeer van ‘grond’ tot ‘geen zuurstof’ meer berekenen. Een weerkundige kan zo een ‘plakje’ atmosfeer uit het weermodel halen en vervolgens bekijken.

Als je deze situatie goed vergelijkt met die van de weerballon dan zien we dat hier ook een grote bak gegevens voor het weer op verschillende hoogtes beschikbaar zijn.

De Skew-T log-P diagrammen zijn dus uitermate geschikt voor het intekenen van deze weergegevens!

Sterker nog, veel ‘gedetailleerde’ weersverwachtingen – ook die van onweer – schrijven we terwijl we een Skew-T naast ons hebben liggen.

In de ‘vaktaal’ geldt er overigens dan nog wel een verschil: waar de Skew-T van de weerballon een sounding wordt genoemd, heet de Skew-T die we bekijken maar die ingetekend is op basis van een berekening van een weermodel anders. Het gaat dan om een progtemp.

Nu we het verschil tussen soundings en progtemps weten kunnen we naar de daadwerkelijke inhoud van een Skew-T kijken! 🙂

De basisingrediënten van een Skew-T diagram

Een Skew-T log-P diagram bestaat uit verschillende zaken die allemaal op één diagram zijn getekend. Deze ‘basisingrediënten’ gaan we hieronder behandelen. Het gaat in het kort om temperatur en dauwpunt, isobaren, isothermen, droog- en natadiabatische lapserates, mixing ratios en windschering.

Dit zijn alle basisingrediënten bij elkaar:

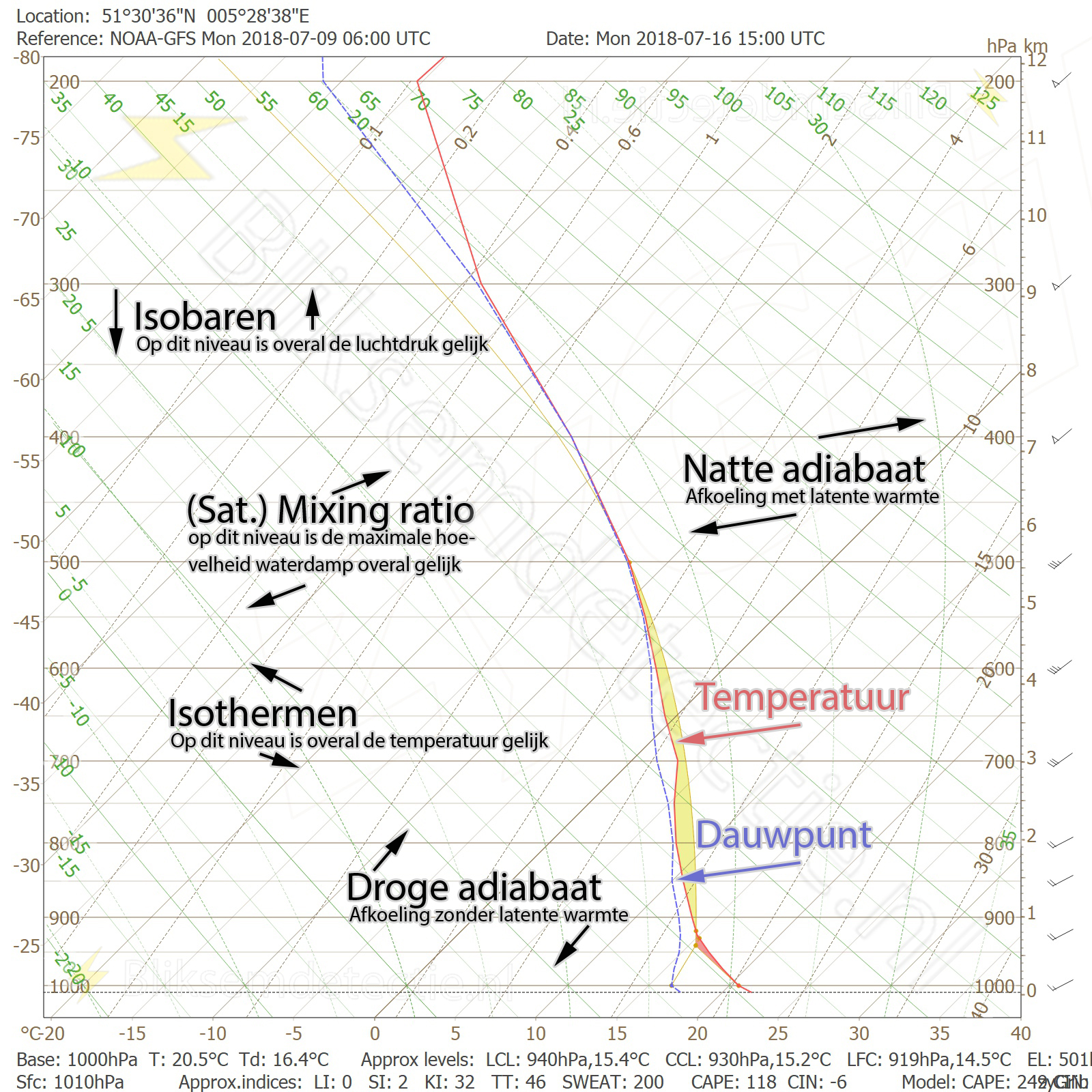
Het is nu niet nodig om het ‘gele vlak’ en het (hele kleine) ‘rode vlak’ te onhouden – dit zijn de CAPE en CAP/CIN, waar we later op terug zullen komen.

En dan nu door met alle losse ingrediënten 🙂

Isobaren

• Op het 500-hPa-drukvlak, “zo’n 5,5 kilometer hoogte”;
• Op 850 hPa, grofweg een kilometer;
• enzovoort!

Deze drukvlakken spelen een rol van betekenis in met name de onweersverwachting.

We kennen allemaal wel het begrip luchtdruk. De lucht om ons heen probeert ons feitelijk ‘weg te duwen’ (het is maar goed dat wij als mensen daartegen bestand zijn). Dat komt doordat de lucht dankzij de zwaartekracht naar de aarde toe wordt getrokken en alles dat ‘in de weg staat’ weg wil krijgen. Dat lukt niet, maar het gevolg is wel dat de atmosfeer continu een druk uitoefent op ons lichaam.

Doordat wij er aan gewend zijn voelen we die niet, maar hij is er toch 🙂

Deze luchtdruk wordt gemeten in de standaardeenheid hectopascal (hPa) en bedraagt gemiddeld gezien aan de grond circa 1000 hPa.

Bij een hogedrukgebied loopt de luchtdruk soms op tot 1050 hPa en bij een lagedrukgebied is 950 hPa geen uitzondering.

Als we omhoog gaan, bijvoorbeeld door een berg te beklimmen, wordt de luchtdruk steeds lager. Boven ons bevindt zich namelijk steeds minder lucht die naar de aarde toegetrokken wordt en daardoor een druk uitoefent op ons lichaam.

Nu we weten hoe de luchtdruk werkt kunnen we doorgaan naar isobaren. Die zijn eigenlijk heel simpel:

De isobaar geeft een lijn van gelijke luchtdruk weer.

Dat kan in de vorm van een weerkaart, waarbij de ‘lijntjes’ van de hoge- en lagedrukgebieden aangeven waar de luchtdruk gelijk is, maar het kan ook op een Skew-T diagram. Het diagram hierboven toont een isobaar, een lijn, waar het overal dezelfde luchtdruk is. Omdat je zo’n lijn ook wel als horizontaal ‘vlak’ kunt zien (in tegenstelling tot het Skew-T-diagram, dat 2-dimensionaal is, is de echte atmosfeer natuurlijk 3-dimensionaal) noem ik het ook wel drukvlak.

Als we rechts kijken op het diagram dan zien we dat de isobaar van het 300 hPa-drukvlak aanwijzen, net als die van 350 hPa.

Richting de grond, aan de onderkant, zien we dat we uitkomen bij de standaardluchtdruk: 1000 hPa.

Dat is echter zo te zien niet de grond, dus op 0 meter is de luchtdruk nog iets hoger (en inderdaad, bij het opslaan van deze Skew-T zaten we onder de rook van een zwak hogedrukgebied).

Het Skew-T-diagram loopt door tot circa 200 hPa: vanaf daar is het eigenlijk weer-technisch niet zo interessant meer, omdat de temperatuur er toeneemt met de hoogte.

Rechts van de ‘luchtdrukken’ zien we ook een schaal met ‘kilometers’: 200 hPa is net iets minder dan 12 kilometer hoogte.

Zo kunnen we meteen achterhalen waar de inschattingen vandaan komen waar we dit deel mee begonnen: 500 hPa is inderdaad grofweg 5,5 kilometer en 800 hPa is inderdaad grofweg een kilometer (1,5 in dit geval).

Het is echter een inschatting, want of we onder een hoge- of lagedrukgebied liggen bepaalt de exacte ‘omrekenfactor’ van hPa naar hoogte. Bij een lagedrukgebied is de luchtdruk aan de grond bijvoorbeeld lager, waardoor we het 500 hPa-vlak ‘eerder’ bereiken – en dan is het dus iets minder dan 5,5 kilometer. Maar bij een flink hoog kan het zo richting de 6 kilometer gaan.

Jullie hebben als het goed is nu door hoe luchtdruk, isobaren en de hoogte in de atmosfeer met elkaar samenhangen. Eerder gaven we aan dat de isobaren (en met name de extra berekeningen die we op die hoogtes kunnen ‘uitvoeren’) een belangrijke rol spelen in de onweersverwachting. Maar het is nog even een klein beetje extra geduld hebben tot we bij die berekeningen zullen komen 🙂 We moeten namelijk eerst verder met de andere basisingrediënten van het Skew-T-diagram. Next up: isothermen!

Tip 1: de isobaren geven de drukvlakken weer in de atmosfeer. Je kunt ze niet direct omrekenen naar hoogte (maar hebt een Skew-T nodig), maar kunt wel vuistregels gebruiken als 500 hPa is ongeveer 5,5 kilometer.

Isothermen

Door naar de isothermen. Waar de isobaren de lijnen van gelijke luchtdruk zijn, geldt voor de isothermen dat het gaat om lijnen van gelijke temperatuur (denk aan een thermometer).

De isothermen staan in een hoek van 45 graden ingetekend in het diagram.

Dat komt doordat met de hoogte de temperatuur afneemt.

Op de verticale as staan de isobaren en dus ook de hoogtes, dus als je een lijn recht omhoog zou trekken betekent het dat je recht omhoog zou gaan, de atmosfeer in.

Je moet dan telkens een lagere temperatuur tegenkomen.

Dat klopt ook: de isotherm die je telkens tegenkomt wijst, als je hem naar beneden volgt, een lagere temperatuur aan – de schaal voor de isothermen vind je aan de onderkant van het diagram.

Op het diagram zijn de temperaturen aangegeven in graden Celcius.

Tip 2: gebruik de isothermen om de temperatuur te achterhalen op een bepaald drukvlak.

Temperatuur en dauwpunt

Zoals we weten van de uitleg hierboven meet een weerballon tijdens de vlucht de temperatuur en het dauwpunt. Natuurlijk is er ook een hoogtemeter ‘aan boord’, waardoor de gemeten temperatuur en dauwpunt gekoppeld kan worden aan een hoogte.

Die worden vervolgens keurig netjes op het Skew-T-diagram geplot, in – zoals we weten – de vorm van een sounding.

Een weermodel kan zo’n vlucht natuurlijk perfect nabootsen, want het berekent immers de volledige stand van zaken in de atmosfeer.

Het is dus ook niet moeilijk om op basis van al deze berekeningen een progtemp in te laten tekenen.

De temperatuur en het dauwpunt zijn de twee lijnen die een sleutelrol innemen in het diagram.

Afhankelijk van of het een sounding of progtemp is, beschrijft de temperatuurslijn, die in het rood wordt weergegeven op het diagram, de gemeten of verwachte temperatuur van de atmosfeer op de hoogte die je afleest.

Isobaren en isothermen zijn hier dus een handig hulpmiddel. Stel dat we vragen: wat is de temperatuur van de atmosfeer op 900 hPa? Het antwoord is: ongeveer 13,5 graden.

We gebruiken allereerst de 900 hPa-isobaar om te kijken op welk punt we de rode temperatuurslijn tegenkomen. Vervolgens trekken we parallel aan de isothermen vanaf dat punt een lijn richting de as aan de onderkant. We zien dan dat we tussen de 10 en 15 graden Celcius uitkomen, op ongeveer ¾ van de afstand. Dat is 13 tot 14 graden. Dat ziet er zo uit, van links naar rechts en onderen:

De dauwpuntslijn beschrijft het gemeten of verwachte dauwpunt van de atmosfeer op die hoogte. Een korte verfrissingscursus over het dauwpunt: op het moment dat lucht afkoelt, neemt de relatieve luchtvochtigheidsgraad van de lucht toe (want koude lucht kan minder vocht bevatten). Op het moment dat de luchtvochtigheidsgraad 100% bereikt condenseert de overtallige waterdamp: er vormt zich dan een wolk of zelfs mist. Dit wordt ook wel ‘dauw’ genoemd – denk aan de dauw (de condens) op het veld in de vroege ochtend. Misschien zie je ‘m al aankomen: het dauwpunt is de temperatuur waarbij, everything else equal, condensatie optreedt en de luchtvochtigheid 100% is.

Als we vragen wat het dauwpunt op een bepaald drukvlak is dan gaat de berekening op dezelfde manier als voor de temperatuur hierboven, maar dan gebruikmakend van de blauwe stippellijn in plaats van de rode temperatuurslijn. Het dauwpunt op 900 hPa is circa 12 graden in het diagram hierboven.

Met name voor onweersbuien is vocht in de atmosfeer van groot belang. Een droge laag ergens in de atmosfeer kan ervoor zorgen dat onweersbuien niet losbarsten. Aan de hand van de temperatuurs- en dauwpuntslijn kun je op een Skew-T diagram heel gauw ‘droge’ spots in de atmosfeer identificeren.

Het verschil tussen temperatuur en dauwpunt op een bepaald drukvlak wordt ook wel dewpoint depression (Tdd) genoemd.

Op het moment dat, op dezelfde hoogte, de temperatuurs- en dauwpuntslijn ver uit elkaar liggen, is er sprake van een lage luchtvochtigheidsgraad en dus een droge laag. Liggen ze dicht bij elkaar, dan is de atmosfeer relatief vochtig. Op het Skew-T diagram hierboven dat de temperatuur- en dauwpuntslijnen met pijlen aanwijst liggen ze overal relatief dicht bij elkaar – behalve onderin de atmosfeer, daar is het iets droger. Aan de grond (bij ca. 0 meter of 1000 hPa) is de verwachte luchtvochtigheid ca. 70-75%. Hoger in de atmosfeer is deze ca. 85%. Bij ‘mixing ratios’ komen we terug op hoe we dit precies berekenen, maar:

Tip 3: op dezelfde hoogte kun je aan de afstand tussen de dauwpunts- en temperatuurslijn een ‘snelle inschatting’ maken of het er relatief droog is. Zo kun je op een snelle manier kijken of ergens in de atmosfeer droge lagen aanwezig zijn, die mogelijk funest zijn voor onweersbuien.

Mixing ratios

Lucht bestaat voor een deel uit waterdamp. Dat is water in de gasfase.

Dat betekent ook dat lucht maar een bepaalde hoeveelheid waterdamp kan bevatten.

Is er meer vocht aanwezig, dan vindt er condensatie plaats en vormt zich een wolk of zelfs mist.

Maar hoeveel waterdamp kan de lucht dan bevatten? En hoeveel waterdamp zit er nu dan in de lucht opgelost?

De mixing ratios zijn bedoeld om antwoord te geven op deze twee vragen.

En dus ook op de vervolgvraag: wat is nu de luchtvochtigheidsgraad?

Er zijn twee soorten mixing ratios:

• Saturation mixing ratios, die aangeven hoeveel gram waterdamp een kilo lucht maximaal kan bevatten;
• Actual mixing ratios, die aangeven hoeveel gram waterdamp er momenteel in een kilo lucht zit opgelost.

Op het moment dat we de mixing ratio willen gebruiken, moeten we eerst een hoogte kiezen.

We kunnen daar zoals we hebben gezien de isobaren voor gebruiken. Laten we het drukvlak van 850 hPa op het diagram kiezen voor de berekening.

Het vinden van de saturation mixing ratio is relatief simpel: we kijken wat de temperatuur is op het 850 hPa-drukvlak en volgen dan de ‘saturation mixing ratio’-lijn omhoog.

Dat ziet er als volgt uit:

Het vinden van de actual mixing ratio is dan ook niet moeilijk. We doen hetzelfde, maar dan gebruikmakend van de dauwpuntslijn:

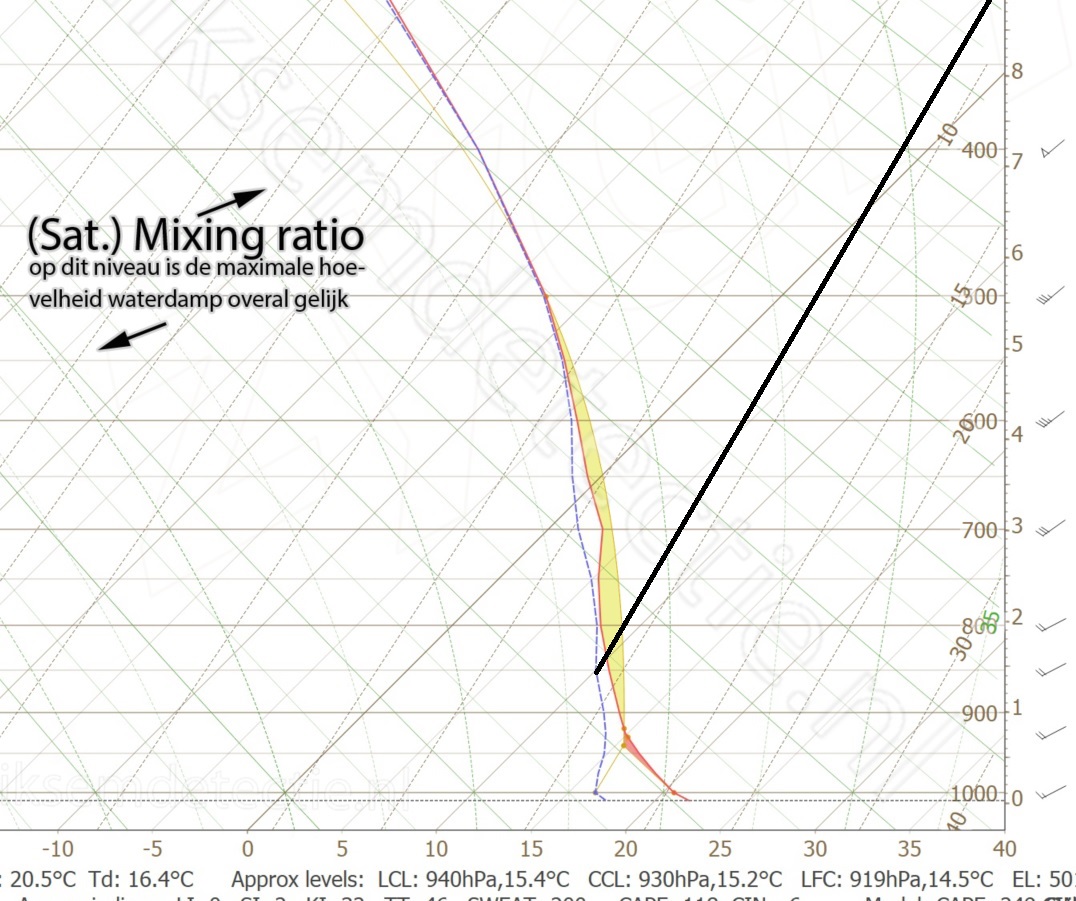
We kunnen de volgende waarden op het diagram aflezen:

• Saturation mixing ratio: circa 9 g/kg;
• Actual mixing ratio: circa 8 g/kg.

Kunnen we nu de luchtvochtigheidsgraad berekenen?

Ja! De luchtvochtigheidsgraad geeft immers het percentage waterdamp in de atmosfeer in verhouding met het maximumpercentage.

Het berekenen van de luchtvochtigheidsgraad komt dan neer op ‘delen van het deel door het geheel maal honderd procent’.

Of in getallen: (8/9) * 100% is ongeveer 88-89%.

Dat komt in de buurt van de schatting van 85% die we hierboven maakten, maar dit is nauwkeuriger bepaald.

Onderin de atmosfeer (op 1000 hPa) was het wat droger, schreven we. We komen daar tot de volgende getallen (maar geven bewust geen afbeeldingen zodat je het zelf kunt oefenen!):

• Saturation mixing ratio: circa 16 g/kg;
• Actual mixing ratio: circa 12 g/kg.

Luchtvochtigheid: 75%! Precies in lijn met onze schatting 🙂

Tip 4: gebruik de mixing ratios om de luchtvochtigheid van een laag te schatten. Zo kun je droge gebieden nauwkeuriger bepalen. De saturation mixing ratio geeft de maximale en de actual mixing ratio geeft de huidige hoeveelheid waterdamp in de atmosfeer aan.

Nog even iets over waterdamp en een lagere temperatuur.

We weten dat koudere lucht minder waterdamp kan bevatten.

Kunnen we dat ook aan de hand van een mixing ratio aantonen?

Jazeker 🙂

Kijk maar eens naar deze diagrammen:

In het eerste zien we de echte saturation mixing ratio voor het 850 hPa-drukvlak van circa 9 g/kg lucht. Aan de isotherm zien we dat de lucht net iets warmer is dan 10 graden Celcius.

In het andere doen we net alsof de lucht afkoelt tot 5 graden Celcius. Uiteraard bekijken we de lucht op hetzelfde drukvlak, dus trekken we een horizontale lijn vanaf de temperatuur op de 850 hPa-isobaar totdat we de 5 graden-isotherm tegenkomen.

Vervolgens trekken we de saturation mixing ratio omhoog.

Het valt buiten beeld, maar de mixing ratio lijn links van onze dikke zwarte lijn geeft op het diagram ‘6 g/kg’ aan (kijk maar op de ‘niet-uitgesneden’ diagrammen).

Oftewel: de saturation mixing ratio op het drukvlak van lucht van 5 graden Celcius is 7 g/kg, en niet meer 9 g/kg zoals bij 10+ graden.

Dat betekent dat er 2 gram per kilogram waterdamp minder in de lucht opgelost kan worden voordat er condensatie optreedt.

Conclusie: koudere lucht kan minder waterdamp bevatten!

Conclusie 2: als we precies het tegenovergestelde zouden doen, dus de lucht laten opwarmen, dan zul je zien dat de lucht méér waterdamp kan bevatten. Dat laten we niet zien… wederom een goede oefening om het zelf te proberen! 🙂

Tip 5: koudere lucht kan minder waterdamp bevatten. Hoeveel waterdamp precies kan worden bepaald door de lucht te laten afkoelen en daarna de saturation mixing ratio te gebruiken.

Windschering: het windverloop

Een ander belangrijk ingrediënt voor onweersbuien is windschering. Hoewel we het later in meer detail uitleggen, is het handig om even te weten wat het is: een veranderende windrichting of -snelheid met de hoogte.

Het gevolg van windschering is dat onweersbuien zich beter kunnen organiseren.

Met zwaardere weersverschijnselen, zoals hagel, veel regen of felle windstoten, als resultaat.

Aan de hand van het windverloop en het hodograph kunnen we informatie vergaren over de windschering.

Het hodograph behandelen we later, maar hiernaast zie je een voorbeeld ‘windverloop’ van het Skew-T-diagram.

Je kunt hiermee ongeveer een inschatting maken in hoeverre er windschering aanwezig is.

Wat we zien zijn windsymbolen vanaf de grond (circa 1000 hPa) tot op 12 kilometer (200 hPa).

Hoe meer streepjes je ziet, hoe harder de wind waait. Vlaggetjes geven een nog sterkere windsnelheid aan.

De windsymbolen wijzen in de richting waar de wind naartoe waait. Op de afbeelding zien we dus een zuidwestelijke wind.

Op het moment dat je omhoog gaat op dit diagram en de windvanen ‘draaien’ sterk, dan is er sprake van een behoorlijke richtingsschering.

Neemt de snelheid significant toe, dan zien we snelheidsschering op de Skew-T staan.

Straks meer over het effect van windschering, voor nu is het voldoende om deze herkenning te kunnen doen!

Windschering: het hodograph

Windschering is ook te herkennen op een hodograph. Dat ziet er zo uit:

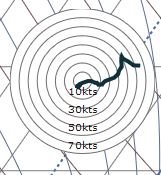
Het diagram toont eigenlijk iets heel simpels: de verandering van windrichting en -snelheid met de hoogte.

De dikke lijn die je op het hodograph ziet, is de combinatie van windsnelheid/windrichting met de hoogte.

We beginnen bij het binnenste punt: dat is de windsnelheid en -richting aan de grond.

De buitenste punt is dezelfde combinatie, maar dan op de hoogte waar de weerballon knapt of waar de progtemp-berekening stopt.

De windrichting is te bepalen door te kijken in welke hoek van het diagram de lijn loopt. De bovenkant is namelijk ‘Zuid’, onderkant ‘Noord’, rechterkant ‘West’ en linkerkant ‘Oost’.

Aan de grond lijkt er dus een ‘noordoostelijke’ wind te staan, naarmate de hoogte vordert wordt de wind steeds ‘zuidwestelijker’.

De windsnelheid (in knopen) op een hoogte kunnen we bekijken door de ‘cirkel’ waar te nemen waar de lijn nu ligt. Aan de grond staat er dus ca. 10 knopen aan wind (ca. 18 kilometer per uur), helemaal bovenin de atmosfeer ca. 65 knopen (120 km/uur).

Op basis van het diagram zien we dat er onderin de atmosfeer wat richtingsschering zit (de wind draait namelijk ergens van noordoost naar zuidwest) en dat de snelheid met de hoogte toeneemt, waardoor er ook wat snelheidsschering staat.

En dat klopt als we het windverloop erbij pakken dat bij dit hodograph hoort:

We weten nu hoe we windschering op een Skew-T-diagram kunnen identificeren!

Maar het moet natuurlijk allemaal wat preciezer als we het effect van de windschering op onweersbuien willen weten.

We gaan straks dan ook kijken of de windschering bijdraagt aan het vormen van buien, d.w.z. welk type bui er zal ontstaan dankzij de windschering;

Next up: het stijgen van een luchtdeeltje! 🙂

Stand van zaken in de atmosfeer

We hebben nu isobaren, isothermen, temperatuur, dauwpunt, (saturated en actual) mixing ratios en wind inclusief windschering langs zien komen. We kunnen nu dus aflezen hoe warm het op een bepaald drukvlak/een bepaalde hoogte is. Ook kunnen we aflezen wat het dauwpunt is, waardoor we een snelle inschatting kunnen maken van droge vlakken in de atmosfeer. Met de mixing ratios kunnen we die inschatting ‘nauwkeuriger’ maken door daadwerkelijk de luchtvochtigheidsgraad op dergelijke hoogtes uit te rekenen.

Dankzij het windverloop en de hodograph kunnen we achterhalen hoeveel windschering er in de atmosfeer aanwezig is. Windschering is een cruciale factor voor onweersbuien die we hieronder nog in veel meer detail zullen bekijken.

Kortom: we kunnen perfect de stand van zaken in de atmosfeer achterhalen aan de hand van het Skew-T-diagram.

Maar dat is niet genoeg om te achterhalen wat de kans is op onweersbuien.

Onweersbuien ontstaan namelijk bij gratie van een stijgend luchtdeeltje. Zonder stijgend luchtdeeltje geen vorming van een stapelwolk en dus ook niet van een onweerswolk.

Zo’n stijgend luchtdeeltje zit echter niet in de basisingrediënten van het Skew-T-diagram verwerkt, want die gingen over de staat van de atmosfeer.

We moeten dus extra zaken toevoegen aan het Skew-T-diagram om een stijgend luchtdeeltje te kunnen modelleren.

We moeten daarvoor kijken naar adiabatische stijging.

Een luchtdeeltje stijgt bij benadering adiabatisch

Zoals we schreven ontstaat een onweersbui bij de gratie van stijgende luchtdeeltjes. Deze luchtdeeltjes kunnen stijgen vanwege verschillende redenen:

• Warmte: de zon kan het aardoppervlak dusdanig verhitten, dat luchtdeeltjes gaan stijgen – de zogeheten thermiek;
• Dynamische forcering: vormen van lagedruk zoals een front, vore/trog of thermisch lagedrukgebied kunnen ervoor zorgen dat er (op grote schaal) stijging van lucht plaatsvindt;
• Orografische forcering: als lucht heuvels of bergen over gedwongen wordt waardoor deze afkoelt en condenseert tot wolken, dan noemen we dit ook wel orografische forcering.

Zoals we weten van het stuk over isobaren ervaart het stijgende luchtdeeltje op een iets hogere hoogte een lagere luchtdruk. Lucht is een gas en op het moment dat de omringende lucht minder hard op het stijgende deeltje drukt, zal het uitzetten. Het volume neemt toe. Een volumevermeerdering kost echter energie. Omdat in de natuurkunde geldt dat een evenwicht altijd wordt hersteld, moet elders energie vandaan worden gehaald om het energietekort weer aan te vullen.

De stijging gaat echter te snel om de energie uit de atmosfeer zelf te halen. Het luchtdeeltje ‘schiet’ als het ware de andere luchtdeeltjes te snel voorbij voor warmte-uitwisseling. Omdat er geen andere warmtebron voorhanden is, moet het deeltje de energie dus uit zichzelf halen om uit te zetten. Dit noemen we een ‘adiabatisch proces’. Warmte uit het deeltje zelf is het snelst voorhanden dus zal gebruikt worden voor deze uitzetting, ook wel ‘adiabatische expansie’ genoemd. Als een luchtdeeltje stijgt koelt het dus af.

De atmosfeer is niet 100% adiabatisch. Er vindt altijd wel een heel klein beetje warmteuitwisseling met de rest van de atmosfeer plaats. Dit is echter onvoldoende om ‘alle’ verbruikte energie weer aan te vullen. De stijging van een luchtdeeltje kunnen we desondanks dus toch adiabatisch benaderen.

Tip 6: lees voor een gedetailleerde uitleg over adiabatische processen en het verschil tussen droog- en natadiabatische stijging onze uitleg over een ‘adiabatisch proces’.

Droogadiabatische lapserates

De eerste fase van de stijging van het luchtdeeltje zal droogadiabatisch verlopen, gebruikmakend van de droogadiabatische lapserate.

We kunnen dit moeilijke woord het beste in drie afzonderlijke delen splitsen:

• Droog: er komt geen vocht vrij bij de stijging;
• Adiabatisch: zonder warmteuitwisseling met de atmosfeer (bij benadering), zoals hierboven uitgelegd;
• Lapserate: een moeilijk Engels woord dat ’temperatuursvervalratio’ betekent, oftewel de afname in temperatuur van het luchtdeeltje (en niet de atmosfeer!) bij een bepaalde stijging, in meters.

Omdat lapserate wat makkelijker schrijft en onthoudt dan temperatuursvervalratio gebruiken we de Engelse term. Het is bovendien een vrij gangbare in de weerwereld. Ik heb in ieder geval nog nooit iemand ’temperatuursvervalratio’ horen zeggen of zien schrijven 🙂

Goed, terug naar de stijging.

Die vindt dus in eerste instantie droogadiabatisch plaats.

Dat komt doordat de luchtvochtigheid vanaf het moment van stijgen niet 100% is, waardoor – zoals we eerder schrijven – er geen condensatie, of ‘dauw’, ontstaat.

Hierdoor is de lapserate (het vervalratio) overal gelijk: de droogadiabatische lapserate is dan ook circa 9,8 graden per kilometer stijging. Als een deeltje een kilometer is gestegen dan is het circa 10 graden koeler.

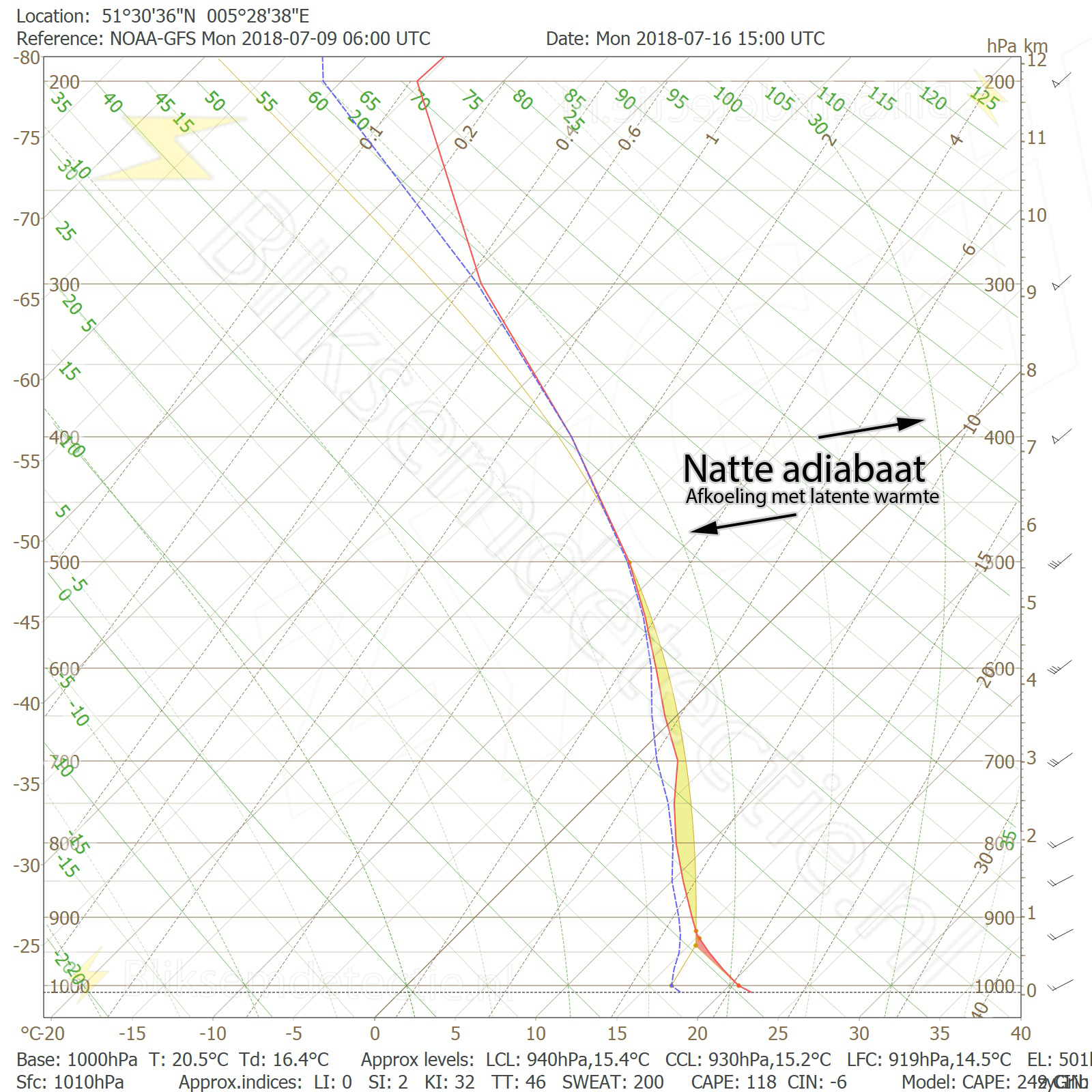
Omdat de droogadiabatische lapserate constant is, wordt deze in de vorm van een ‘rechte lijn’ weergegeven in het Skew-T-diagram (zie de afbeelding hierboven). De lijnen lopen links omhoog, omdat het gaat om afkoeling.

De vraag die nu nog heerst is: hoe kunnen we een droogadiabatische stijging van een luchtdeeltje modelleren? Simpel. Als we ervan uitgaan dat een deeltje vanaf de grond stijgt (dit hoeft niet altijd zo te zijn), dan kunnen we vanaf dit punt de droogadiabatische lijn volgen:

Simpel & nu hebben we de stijging van het luchtdeeltje te pakken!

Of toch niet?

…we vergeten iets, maar wat?

Natadiabatische lapserates

Het antwoord: de condensatie 🙂

Van de uitleg over adiabatische stijging hierboven weten we dat het stijgende luchtdeeltje afkoelt naarmate het verder stijgt.

Uit het deel over mixing ratios weten we dat de luchtvochtigheid toeneemt op het moment dat de temperatuur afneemt.

Op een bepaald moment tijdens de droogadiabatische stijging is de luchtvochtigheidsgraad 100%.

De lucht condenseert dan en een wolk begint zich te vormen.

Dit punt wordt ook wel het Lifting Condensation Level (LCL) genoemd.

Het is ook het punt waar onze vergetelheid problematisch begint te worden 🙂

Hierboven schreven we dat de droogadiabatische lapserate circa 9,8 graden per kilometer is. Dat is een constante daling van de temperatuur als het luchtdeeltje stijgt. Er is nu echter één probleem: bij condensatie komt warmte vrij.

Hoe dat werkt is relatief simpel. Bij condensatie vindt er een overgang plaats van de gas- naar de vloeistoffase. Watermoleculen hebben een bepaalde hoeveelheid ‘bewegingsenergie’ in zich, zodat ze een gas zijn. Ze kunnen als het ware iets vrijer bewegen. Op het moment dat er een vloeistof van wordt gemaakt kun je het ‘vangen’ in bijvoorbeeld een glas. De bewegingsvrijheid van water is dus iets minder groot dan die van waterdamp. Om van een gas (waterdamp) naar vloeistof (waterdruppeltjes in de wolk) te gaan moet er dus een beetje van deze ‘bewegingsenergie’ worden weggehaald. We weten van eerder in dit artikel dat de natuur altijd probeert om een evenwicht te herstellen. Dat doet het in dit geval door deze ‘bewegingsenergie’ vrij te laten in de atmosfeer, in de vorm van warmte.

Het vrijkomen van warmte bij de condensatie van lucht wordt ook wel latente warmte genoemd.

Waarom is dit problematisch, denk je nu misschien?

Op het moment dat er warmte vrijkomt, is de afkoeling van de lucht bij stijging niet meer gelijk aan 9,8 graden Celcius per kilometer.

We kunnen dus zeggen dat er vanaf het LCL een nieuwe vorm van stijging plaatsvindt. Dat is droogadiabatische stijging ‘plus’ de latente warmte. We noemen dit ook wel natadiabatische stijging (er komt immers vocht vrij).

Deze stijging kent ook z’n eigen lapserate. Die is echter niet constant. Dat komt namelijk omdat de hoeveelheid condensatie sterk afhangt van de temperatuur. Hoe kouder, hoe meer condensatie. Dat heeft effect op de lapserate. Grofweg kunnen we zeggen dat circa 5 graden per kilometer realistisch is, maar het is gegarandeerd niet accuraat. Het Skew-T diagram houdt er dan ook rekening mee en modelleert de natadiabatische lapserates als ‘krommes’.

We kunnen nu dus een volledige stijging modelleren! We vergeten nog één ding: het Equilibrium Level (EL). Op dit punt is de temperatuur van de atmosfeer, die voorheen altijd koeler was, weer gelijk aan het stijgende luchtdeeltje. Daarna neemt deze toe. Het is dus het ‘hoogste punt’ tot waar het luchtdeeltje kan stijgen, want warme lucht stijgt en koude lucht daalt. Na het EL is het luchtdeeltje kouder dan zijn omgeving. Het stijgen houdt dan op.

Hoe we het LCL, het EL en ook het zogeheten Level of Free Convection (LFC), een ander belangrijk punt voor het inschatten van onweersbuien, precies op het Skew-T-diagram kunnen detecteren – dat behandelen we verder naar onderen.

Maar voor nu is het genoeg om te weten dat een stijgend luchtdeeltje eerst de droogadiabatische lapserate volgt, vanaf het LCL de natadiabatische, waarna het doorstijgt tot het EL.

En dat ziet er dan zo uit. Vanaf de grond laten we het deeltje eerst droogadiabatisch stijgen middels de droogadiabatische lapserate; vanaf het LCL gaan we over op de natadiabatische lapserate. Op het EL stopt de stijging.

We hebben nu de volledige ‘basis’ onder de knie om te kijken naar het gebruik van Skew-T’s bij onweersituaties! Maar eerst iets over de moeilijke naam van het diagram 🙂

Herkomst van de naam Skew-T log-P

Het is wel een beetje een bijzondere naam: Skew-T log-P diagram.

Waar komt die naam vandaan?

Er is eigenlijk een hele logische verklaring voor die moeilijke naam 🙂

Als we naar de basisingrediënten hierboven kijken:

• Dan zien we dat de isothermen, de lijnen met gelijke temperatuur in de atmosfeer, in een hoek van 45 graden ten opzichte van het diagram getekend zijn. De isothermen geven de temperatuur aan, dus de “T”. Een dergelijke kanteling in een hoek heet in het Engels ook wel “skewed” – vandaar Skew-T.
• Op de verticale as zien we de luchtdruk getekend staan: van circa 1000 hPa tot 0 hPa. Hiervoor wordt een logaritmische schaal gebruikt. Dat betekent in het geval van de Skew-T dat de afstand tussen 1000 en 900 hPa “kleiner” is dan de afstand tussen 100 en 0 hPa. Dat komt doordat de luchtdruk logaritmisch met de hoogte afneemt. Luchtdruk is “Pressure” (P) in het Engels… en vandaar de naam log-P!

En zo wordt het eigenlijk heel snel duidelijk waarom het diagram zo’n makkelijk moeilijke naam heeft 🙂

Noodzakelijke ingrediënten voor onweersbuien

Een stijgend luchtdeeltje betekent echter geen onweersbui. Dat zou niet best zijn – dan zou namelijk ieder doorstijgend luchtdeeltje uitgroeien tot een onweer & zouden we de zon nooit meer zien! 🙂

Er zijn dus bepaalde factoren die in de atmosfeer aanwezig moeten zijn wil het tot echte onweersbuien komen.

Het vervelende van al deze factoren is dat ze in precies de juiste combinatie aanwezig moeten zijn, want anders gaat het mis. Het kan niet zo zijn dat er één ‘wegvalt’ en dat de rest dan voldoende is om het op te vangen. Nee, meestal – en al helemaal bij een potentieel zware onweerssituatie – is het alles of niets.

Het gaat concreet om de volgende ingrediënten:

• Onstabiliteit;
• Omgekeerde onstabiliteit;
• Trigger;
• Windschering.

Onstabiliteit

Een bui gaat pas onweer produceren op het moment dat ijskristallen met elkaar botsen, waarna een spanningsverschil ontstaat binnen of buiten de wolk.

Dat betekent dat het stijgende luchtdeeltje – en dus uiteindelijk de wolk – ver genoeg moet groeien om ‘ijzig’ te worden (te herkennen aan het ‘wit’ van de wolk).

Wat daarvoor nodig is, is een hele boel onstabiliteit. Vergelijk het met een vuurwerkshow die opgesteld staat: er is een hele boel ‘energie’ voorhanden. Als de show wordt aangestoken, zien we een fraai spektakel in de lucht – dankzij de energie. De onstabiliteit werkt net zo: het geeft aan hoe ‘welwillend’ de atmosfeer is ten aanzien van stijgende lucht. Bij een hele hoge onstabiliteit kunnen (mits de buien ontstaan!) onweersbuien zeer fel uitpakken.

De (potentiële) onstabiliteit wordt ook wel berekend als Convective Available Potential Energy (CAPE). Het gaat om energie, dus de waarde is ‘Joules’ (J) per kilogram lucht (J/kg). Waarden van meer dan 1500 J/kg geven voor Nederlandse begrippen een behoorlijk onstabiele situatie aan; 2000 J/kg of meer en de atmosfeer is hoogst explosief. Bij heel zwaar potentieel onweer komen CAPEs van 2500 J/kg en hoger voor.

Op www.wxcharts.eu kun je snel en overzichtelijk kaarten met actuele CAPE bekijken.

Omgekeerde onstabiliteit

In tegenstelling tot onstabiliteit houdt omgekeerde onstabiliteit het ontstaan van onweersbuien tegen.

En dat is een goed iets.

Deze omgekeerde onstabiliteit, die ook wel inversie of ‘capping layer’ wordt genoemd en kan worden uitgedrukt in CIN (Convective Inhibition, een soort omgekeerde CAPE), is namelijk een soort ‘deksel op de pan’.

We weten dat als de atmosfeer onstabiel is, het deeltje verder kan stijgen. Dat betekent dus dat de temperatuur van het deeltje warmer is dan de temperatuur van de atmosfeer op een bepaalde hoogte.

Soms gebeurt het echter dat ergens tussen begin en eind (het EL) de temperatuur van de atmosfeer even hoger is dan die van het stijgende luchtdeeltje.

Oops, dan houdt daar de stijging op. Het “deksel zit nog op de pan”.

Dat is echter goed voor felle onweersbuien. Op het moment dat het niet had gebeurd, dan hadden de kleinste stapelwolken uitgegroeid tot buien. Even leuk, maar het betekent ook dat het zonlicht het aardoppervlak niet continu kan verwarmen (de warmte die er is regent weer weg met de buien). Gevolg: het blijven kleine buitjes, en that’s it.

Op het moment dat de inversie een deksel vormt over de onderste laag van de atmosfeer, zien we dat het flink begint te borrelen daar in dat kleine deel. Tot op een bepaald moment een aantal stijgende luchtbellen door de inversie heen breken. Ze knallen dan direct omhoog tot 12 kilometer hoogte en misschien zelfs wel verder! De energie (CAPE) die namelijk is opgebouwd, is enorm 🙂

De verschillende triggers die we zometeen gaan beschrijven zijn in staat om lucht ‘boven deze laag’ uit te tillen, waarna het ontstaan van buien kan beginnen.

Tijdens situaties waarin er kans is op zwaar onweer zien we dus graag een capping layer aanwezig zijn tijdens de eerste helft van de dag, terwijl deze na het middaguur verdwijnt door één van de hieronder beschreven triggers. Onweersbuien kunnen op dergelijke momenten behoorlijk fel uitpakken.

Trigger

We mogen dan wel een boel energie hebben bij die vuurwerkshow, maar als hij niet aangestoken wordt gebeurt er dus niets. We hebben dus een lont nodig, die in de weerwereld ook wel trigger wordt genoemd.

De trigger zorgt ervoor dat de lucht boven het Level of Free Convection (LFC, het niveau waarbij lucht ongeremd verder kan stijgen tot het Equilibrium Level) uitkomt. Hierdoor kan de lucht zoals gezegd ongeremd doorstijgen. Het LFC behandelen we later in meer detail.

Er bestaan verschillende soorten triggers zoals we ook al bij de uitleg over het adiabatische proces hebben gezien:

• Warmte: de zon schijnt op het aardoppervlak, waarna de kortgolvige zonnestraling wordt omgezet in langgolvige straling. Dat is warmte. Warmte voelen wij aan een heerlijke temperatuur, maar natuurlijk gebeurt er meer. De warme lucht is namelijk geneigd om te stijgen, omdat de dichtheid ervan lager is dan die van de iets koelere lucht erboven. Deze thermiek is zeer gewenst voor zweefvliegers. Op het moment dat de warmte krachtig genoeg is, kan de lucht zelfs boven het LFC uitkomen, waarna een stapelwolk doorgroeit tot bui – en afhankelijk van de onstabiliteit en sterkte van de ‘updraft’ zelfs tot onweersbui.
• Lagedruk: een vorm van lagedruk kan ervoor zorgen dat de lucht boven het LFC uitkomt. Er bestaan verschillende vormen:
  • Een front, in de regel een koufront, brengt koude lucht naar ons land. Deze koude lucht ‘wringt’ zich vanwege dezelfde regel (koud onder warm) onder de warmere lucht, waardoor deze moet stijgen. Is het front ‘scherp’ genoeg en moet de warme lucht relatief snel stijgen naar middelbare hoogte, dan kan het zijn dat deze boven het LFC uitkomt waarna buien ontstaan.
  • Een trog of vore kunnen ook voor onweersbuien zorgen. Beiden zijn uitlopers van een bestaand lagedrukgebied. Dat wil zeggen dat er een ‘klein beetje’ lagere druk begint te vormen, maar dat het nog geen volwassen lagedrukgebied is. Lagedruk betekent stijgende lucht, met als gevolg dat op dergelijke gebieden vaak onweersbuien ontstaan.
  • Een thermisch lagedrukgebied. Dit is vrijwel hetzelfde als ‘warmte’ maar dan op grote schaal. Er ontstaat geen ‘enkele’ onweersbui door de warmte, maar doordat een groot gebied wordt opgewarmd stijgt de lucht er tegelijkertijd. Het gevolg: er ontstaat een lagedrukgebied in de onderste lagen van de atmosfeer. Dit proces is krachtig genoeg om lucht grootschalig boven het LFC te brengen. Bij een thermisch laag ontstaan er dus meestal behoorlijk wat onweersbuien, die soms heel zwaar kunnen worden!
• Orografische triggering (d.w.z.: bergen en heuvels): bij bergen en heuvels wordt de lucht ‘over’ de berg gedwongen. Als hij namelijk aan komt waaien en de berg tegenkomt, kan hij niet naar links (daar hangt dezelfde luchtsoort) noch naar rechts (idem dito). Hij kan ook niet terug: daar komt nieuwe lucht vandaan. Hij moet dus wel over de berg heen, waardoor hij gedwongen wordt te stijgen. Het gevolg: condensatie & mogelijk felle onweersbuien!

De trigger geeft de lucht dus als het ware een ‘zetje’ omhoog. Maar de aanwezigheid ervan is geen garantie op onweer. Is er ‘omgekeerde onstabiliteit’ d.w.z. een inversie aanwezig? Hoe sterk is de trigger? Ligt er nog hogedruk in de buurt die ’t allemaal wat tegenhoudt? Het zijn allemaal factoren die beïnvloeden of er wel of geen onweersbuien ontstaan. Oftewel:

Tip 7: Er is een trigger nodig voor het ontstaan van onweersbuien, maar de aanwezigheid van een trigger betekent niet een garantie op onweer.

Windschering

We hebben nu dus een vuurwerkshow, maar hoe zwaar wordt die vuurwerkshow?

Dat hangt af van hoeveel combinaties aan vuurwerk worden ingezet.

Als vervolgens het vuurwerk ook nog eens alle kanten opschiet (binnen de veiligheidsmarge uiteraard), dan wordt het spektakel alleen maar groter.

De windschering speelt hier een rol. Dat heeft alles te maken met de omhooggaande stroom warme lucht in de bui (de updraft) en de neergaande stroom lucht (de downdraft): samen vormen ze een combinatie. De updraft ontstaat eerst, vormt de bui en houdt hem enige tijd in stand, waarna het gaat regenen en de downdraft ontstaat.

Maar deze downdraft ‘snijdt’ als het ware de warme lucht die de bui in moet af, omdat de koude lucht aan de grond blijft hangen.

Het gevolg is dat de bui een snelle dood sterft en het is een vrij normaal verschijnsel in de levenscyclus van buien.

Maar windschering kan ervoor zorgen dat dit wordt uitgesteld. Windschering is als het ware het veranderen van de windsnelheid en/of windrichting met de hoogte. Het veranderen van windsnelheid wordt ook wel ‘snelheidsschering’ genoemd; het veranderen van windrichting ook wel ‘richtingsschering’.

Bij een hele sterke windschering kunnen er felle fenomenen ontstaan:

• Grote hagelstenen;
• Een supercel;
• Een tornado;
• Heftige windstoten.

Is de windschering echter té sterk, dan kan het zijn dat de buien al uit elkaar waaien voordat ze goed en wel op gang zijn gebracht.

Nu we weten wat de ingrediënten zijn voor een onweersbui, hoe we een Skew-T-diagram kunnen interpreteren en er een luchtdeeltje op kunnen laten stijgen, kunnen we kijken naar een ietwat geavanceerder deel van Skew-T’s: het aflezen van onweerparameters en het verbinden van conclusies daaraan gegeven een onweersituatie. Let’s go!

Onweerparameters aflezen op een Skew-T

Nu we weten hoe een Skew-T log-P diagram eruit ziet kunnen we een aantal veelgebruikte ‘onweerparameters’ behandelen. Deze zijn stuk voor stuk op het Skew-T diagram af te lezen. Ze zeggen iets over de stand van zaken in de atmosfeer, in het geval van de sounding over de huidige atmosfeer en in het geval van de progtemp de verwachte atmosfeer. Samen geven ze een heel goed beeld van wat er mogelijk is tijdens een onweerssituatie 🙂 We behandelen:

• Het LCL (Lifted Condensation Level);
• Het LFC (Level of Free Convection);
• Het EL (Equilibrium Level) / tropopauze;
• CAPE;
• Lifted Index;
• Windschering: het type bui, middels het hodograph.
• Total Totals;
• K-Index;
• De ‘cap’ en dus CIN.

Tijd om de onweersituatie te beschrijven.

Er is kans op zwaar onweer in Donderdorp

Laten we een realistische maar relatief ‘simplistische’ (geen gepriegel dus) onweerssituatie beschrijven.

We zitten in Donderdorp en de weerlieden spreken al dagen over het feit dat het vandaag wel eens behoorlijk kan gaan onweren. Er ligt namelijk een uitloper van een lagedrukgebied in de buurt dat voor onweersbuien kan gaan zorgen. Bovendien zou er veel onstabiliteit zijn en toch ook enige windschering.

Maar klopt het wel wat de weermensen zeggen? Hieronder gaan we het bekijken aan de hand van het Skew-T-diagram voor Donderdorp!

We stellen ons de volgende twee vragen:

1. Kan er vandaag in Donderdorp een onweersbui ontstaan?
2. Als er een onweersbui ontstaat, hoe zwaar wordt hij dan?

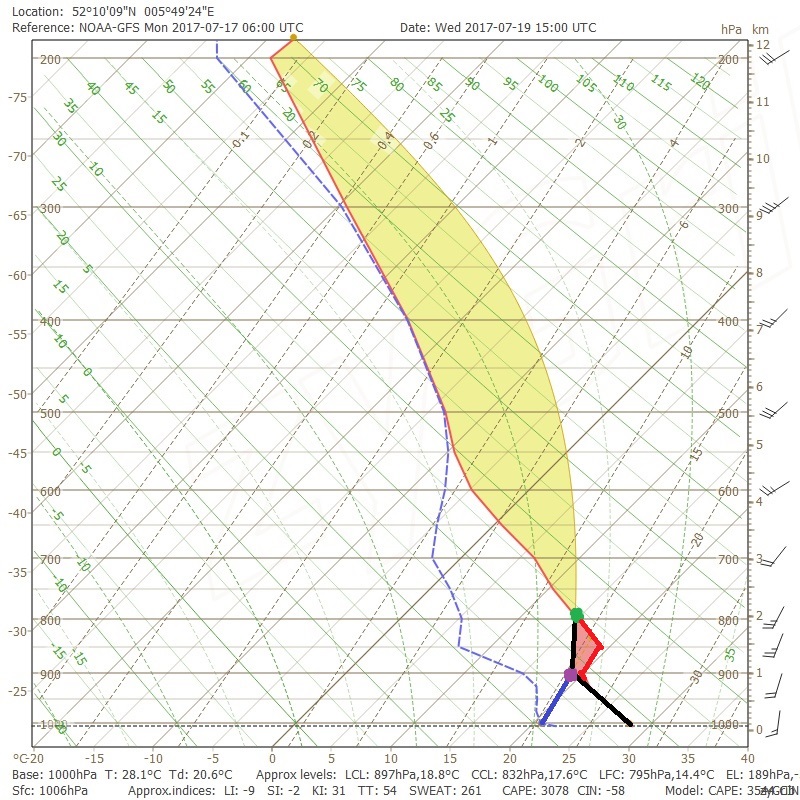
Hier is de Skew-T:

Kan er een onweersbui ontstaan?

We herinneren ons de drie ingrediënten voor onweer:

• Voldoende onstabiliteit;
• Een trigger die voldoende doorzet;
• Voldoende dynamiek d.w.z. windschering.

De dynamiek is met name van belang om te kijken hoe zwaar de bui uitpakt. Daar komen we dus straks op terug. De twee ingrediënten onstabiliteit en trigger zijn echter wat we hieronder gaan bestuderen! Zou het lukken met het onweer?

Het LCL: Lifted Condensation Level

De atmosfeer in Donderdorp is dus behoorlijk onstabiel. Bovendien zit er een ‘capping layer’ in de onderste lagen van de atmosfeer, waardoor we te maken kunnen krijgen met zeer fel onweer als de trigger voldoende sterk is.

Het Lifted Condensation Level (LCL) is zoals we weten de hoogte waarop condensatie plaatsvindt. Dat is dus de hoogte waar de wolk begint te groeien als de trigger sterk genoeg is; feitelijk dus de onderkant van de bui. De wolkenbasis van een onweerswolk zit dus grofweg ter hoogte van dit LCL.

We weten nog hoe stijging in zijn werk gaat:

1. Een deeltje stijgt droogadiabatisch;
2. Dit gaat net zo lang door tot de luchtvochtigheid 100% wordt.

Als we een luchtdeeltje laten stijgen, neemt de temperatuur dus af volgens de droogadiabatische lapserate.

We weten ook dat we aan de hand van de temperatuur op een bepaalde hoogte de ‘saturation mixing ratio’ kunnen bepalen, dus de maximale hoeveelheid waterdamp die een kilo lucht daar kan bevatten.

De vraag is nu: op welke hoogte is de temperatuur van het stijgende luchtdeeltje gelijk aan deze saturation mixing ratio? Dus: op welke hoogte is de temperatuur van het stijgende luchtdeeltje zo, dat hij de maximale hoeveelheid waterdamp bevat?

De tekening is heel simpel:

1. We tekenen de droogadiabatische stijging van het deeltje – de temperatuur koelt af volgens de droogadiabatische lapserate;
2. Vanaf het actuele dauwpunt (de temperatuur aan de grond waarbij de saturation mixing ratio wordt behaald) volgen we de saturation mixing ratio-lijn, om dezelfde stijging te benaderen;
3. Op het snijpunt van deze lijnen is de temperatuur van het stijgende luchtdeeltje gelijk aan de temperatuur waarvoor het saturation mixing ratio wordt gehaald.

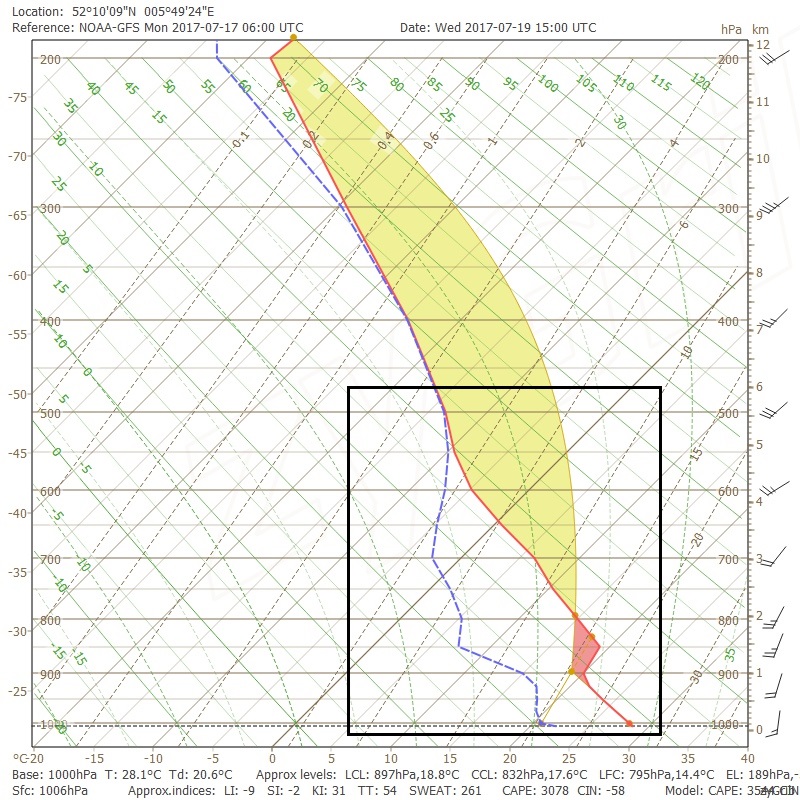
Dit snijpunt, hieronder met een dikke paarse vlek aangegeven (de mixing ratio is blauw en de droogadiabatische stijging zwart), is het Lifting Condensation Level, het condensatieniveau! Het ligt op zo’n 900 hPa, dus een kilometer hoogte. Dat is redelijk hoog, maar niet té hoog.

Het LFC: Level of Free Convection

Vanaf het LCL condenseert de stijgende lucht. Daar komt zoals we weten latente warmte bij vrij, waardoor we vanaf dat moment de natadiabatische lapserate moeten volgen. Maar dat lucht condenseert betekent nog niet dat er onweer komt.

Sterker nog: het zou zomaar kunnen zijn dat het enkel stapelwolken blijven.

Het wordt dus zaak om de volgende stap te zetten. Dat is in ons geval het Level of Free Convection (LFC).

Zoals de naam al doet vermoeden, is dit het punt waarop stijgende lucht geen trigger meer nodig heeft, en dus vrijelijk verder kan stijgen.

Het is dus in het voordeel van onweersbuien als dit punt zo laag mogelijk in de atmosfeer ligt.

Maar hoe achterhalen we het?

Dat is ook vrij logisch.

We hebben net het LCL gevonden middels droogadiabatische stijging en weten dat vanaf dat punt de lucht natadiabatisch verder stijgt.

Laten we dat dan ook doen.

We volgen de natadiabatische lapserate en gaan verder omhoog.

Nu maken we even een denkstap in wat meer abstracte zin:

Wanneer kan lucht vrijelijk stijgen?

Het antwoord is enorm simpel en hebben we al een aantal keren langs zien komen: wanneer de lucht warmer is dan de omringende lucht!

In het geval van de atmosfeer boven Donderdorp: wanneer het stijgende luchtdeeltje warmer is dan de omgeving!

Tijdens de gehele droogadiabatische stijging hebben we gezien dat het niet zo is. De temperatuurlijn lag namelijk ‘links’ van de adiabatische lijn, hetgeen als we de isothermen volgen betekent dat de atmosfeer warmer is dan het stijgende luchtdeeltje.

Geen vrije stijging dus.

Maar dat betekent ook dat het luchtdeeltje vrij verder kan stijgen vanaf het moment dat de stijgingslijn zélf boven de temperatuurlijn zit!

Et voila: als we de natadiabatische stijging op het diagram intekenen zien we dat dit gebeurt rond 800 hPa, zo’n 2 kilometer.

We zetten hier een dikke groene punt neer: we hebben het LFC gevonden! Goed te zien is dat als we verder adiabatisch zouden stijgen (het gele lijntje volgen vanaf de groene punt; de natte adiabaat) de temperatuur van het stijgende deeltje ‘rechts’ van de atmosfeertemperatuur ligt. Het stijgende deeltje is vanaf dat moment dus warmer, met vrije stijging als gevolg!

Een pauzemomentje waarin we de situatie van Donderdorp analyseren. Tussen het LCL en het LFC zit dus circa een kilometer. Dat betekent dat we een trigger nodig hebben die dit verschil kan overbruggen!

En voor wat betreft trigger houden we het kort: zoals de weerlieden aangaven ligt er een vore, een uitloper van een lagedrukgebied, in de buurt! Voor nu kunnen we ervan uitgaan dat deze sterk genoeg is om het tot onweer te laten komen (dat maakt het iets makkelijker 🙂 )

De CAP en CIN

We schreven eerder al dat een belangrijk ingrediënt voor onweersbuien omgekeerde onstabiliteit was.

Dat klinkt natuurlijk raar: je hebt toch onstabiliteit nodig om onweersbuien hard te laten groeien, zodra ze zijn ontstaan?

Dat klopt!

Maar omgekeerde onstabiliteit is ook een essentieel onderdeel van felle onweersbuien.

Dat wordt duidelijk op het moment dat je de onweersituatie vergelijkt met een snelkookpan.

Als je de snelkookpan op het vuur zet en het water aan de kook brengt, dan zien we overal belletjes – logisch, want het water kookt.

Maar daar blijft het bij.

Op het moment dat je vervolgens de deksel op de pan legt, bouwt zich een grote druk op onder de deksel. De waterdamp wil weg!

En zo gaat het ook een beetje in zijn werk bij omgekeerde onstabiliteit. Deze vorm, die ook wel een inversie wordt genoemd, betekent dat een deeltje nog niet ‘vrij’ kan stijgen doordat de temperatuur van het stijgende deeltje lager is dan de temperatuur van de atmosfeer rondom de stijgende luchtbel.

Uit de voorgaande tekst weten we dat dit het stuk is tussen het LCL en het LFC.

Het fungeert als het ware als een deksel op de pan waarbij het allerlaagste deel van de atmosfeer als water fungeert: dankzij het deksel kan de lucht nog niet verder stijgen, maar dankzij het zonlicht warmt het al wel flink op… het borrelt… maar het kan nog niet knappen!

Het deksel wordt ook wel capping layer, afgekort CAP genoemd.

Pas op het moment dat de luchtbel door de inversie heen kan breken, en het LFC bereikt, kan de lucht vrij verder stijgen. En het gaat dan enorm snel! Er heeft zich immers over de dag heen een enorme hoeveelheid energie opgebouwd.

Vaak helpt een trigger in de vorm van lagedruk (trog, vore, front, …) om de lucht boven de inversie uitgetild te krijgen. Is deze niet sterk genoeg, dan kan de inversie soms niet worden doorbroken. Dit is een veelvoorkomende reden waardoor er soms toch zwaar onweer op de kaarten staat, maar het uiteindelijk reuze meevalt.

De omgekeerde onstabiliteit drukken we uit in Convective Inhibition, ook wel CIN (en soms CINH) genoemd. Net als de CAPE is de eenheid van de CIN J/kg, maar dan ‘in de omgekeerde’ richting (het gaat om omgekeerde onstabiliteit).

Op het Skew-T is de CIN het oppervlak tot aan het LFC tussen temperatuurslijn en de lijnen van adiabatische stijging. Feitelijk het rode deel dus!

Droogte in de atmosfeer

Een ander belangrijk fenomeen voor het ontstaan van onweersbuien is de hoeveelheid vocht in de atmosfeer.

Hoe meer vocht er is, hoe sneller er condensatie plaatsvindt. Hoe meer vocht er is op hoogte, hoe meer condensatie er daar vrijkomt, waardoor latente warmte (de natadiabatische stijging!) vrijkomt en het deeltje nog net iets verder kan stijgen.

Meer vocht is dus goed voor het groeien van onweersbuien.

Als we de kans op onweer inschatten moeten we dus bij het bepalen of er een bui kan ontstaan ook goed kijken naar de droogte in de atmosfeer.

Is het te droog, dan kan de atmosfeer op hoogte nog wel onstabiel zijn, maar dan komt e.e.a. nooit van de grond.

We weten dat we de droogte kunnen meten middels de dauwpuntsdepressie, dus het verschil tussen temperatuur en dauwpunt op een isobaar.

Hoe groter dit verschil, hoe droger de atmosfeer op die hoogte.

Op het Skew-T-diagram voor Donderdorp zien we dat we te maken hebben met een behoorlijk droge atmosfeer.

We moeten hiermee rekening houden, want het kan zomaar eens een fel onweer tegenwerken!

Het tempert tot nu toe de verwachting een beetje 😉

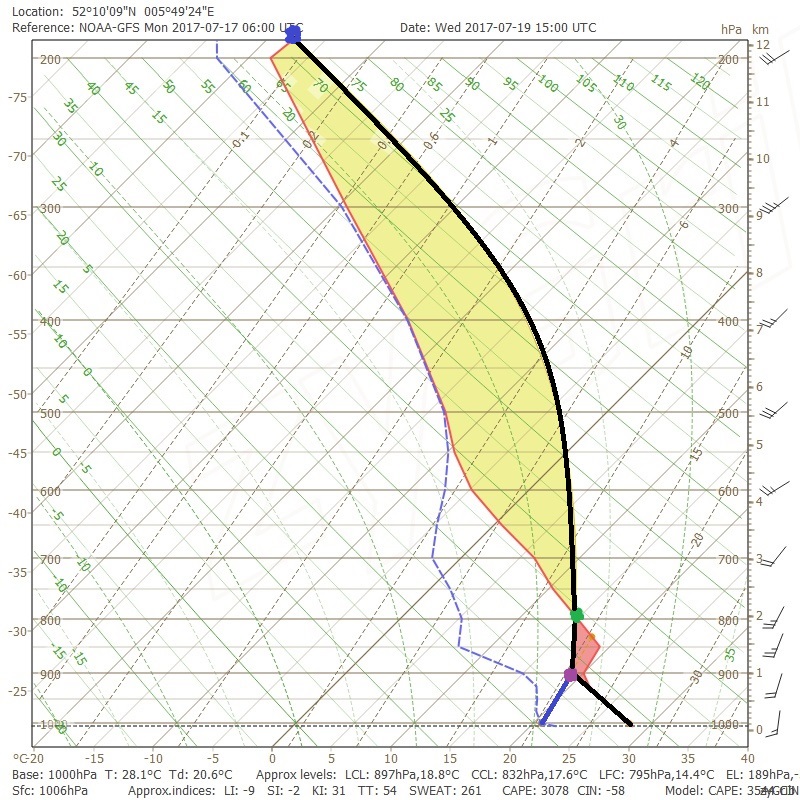Het EL: Equilibrium Level

We weten dat lucht dankzij verschillende triggers boven deze ‘cap’ uit kan komen. Vanaf het moment dat het LFC bereikt wordt kan de lucht vrijelijk verder stijgen. Stel dat dit gebeurt.

Tot welke hoogte kan de lucht dan stijgen?

Niet tot in de ruimte, dat zal wellicht wel logisch zijn.

Het punt waarop de lucht weer stopt met stijgen noemen we het Equilibrium Level (EL). De temperatuur van een (nat)adiabatisch stijgend luchtdeeltje is op dat moment weer gelijk aan de temperatuur van de omliggende atmosfeer.

Steken we ons hoofd vlak boven dat niveau, dan is de atmosfeer weer warmer dan het deeltje. Het deeltje kan dus simpelweg niet verder stijgen (enkele uitzonderingen, zoals de ‘overshooting top’, daargelaten).

Hoe vinden we dit EL op het Skew-T-diagram?

Heel simpel: vanaf het LFC laten we het deeltje natadiabatisch verder stijgen totdat we de temperatuurlijn weer snijden.

Dat gebeurt in het Skew-T van Donderdorp op zo’n 12 kilometer hoogte, bij de blauwe stip. Dat is helemaal aan de bovenkant van de troposfeer.

Als een luchtdeeltje dus boven het LFC weet uit te komen kan het vrijelijk doorstijgen tot 12 kilometer hoogte – wat lijkt te neigen naar zware onweersbuien.

Maar daarvoor moeten ze wel ontstaan. Dat is een belangrijke eis!

De verwachte kracht van onweersbuien kunnen we echter inschatten door naar het begrip CAPE te kijken. Dat schetst de onstabiliteit, en hoe onstabieler de atmosfeer, hoe meer energie ze hebben om fel uit de hoek te komen.  Drie keer raden wat we nu gaan doen… 😉

CAPE

We weten dat onstabiliteit een belangrijk ingrediënt is voor onweersbuien. CAPE, dat staat voor Convective Available Potential Energy, kunnen we gebruiken om de onstabiliteit van de atmosfeer aan te geven.

De CAPE wordt uitgedrukt in Joules energie per kilogram lucht, dus J/kg. CAPEs van 1000 J/kg en hoger zien we vaak bij onweersbuien; 2000 J/kg en hoger bij zware onweersbuien, en heel soms 2500 J/kg+ bij zeer zware exemplaren.

Uiteraard liggen de CAPEs in de Verenigde Staten nog veel hoger (CAPEs van 8000+ J/kg zijn daar geen uitzondering), maar we zitten natuurlijk in Nederland 🙂

Hoe bepalen we de CAPE?

Dat doen we door het stijgende luchtdeeltje adiabatisch door te laten stijgen tot het EL en vervolgens met een integraalberekening het oppervlak berekenen tussen de temperatuurlijn en natte adiabaat tussen het LFC en het EL.

Dat is dus het gele vlak op het diagram.

En wees niet bang, dat kan geen mens uit zijn hoofd 🙂

Daarom wordt de CAPE meestal al uitgerekend op het Skew-T-diagram in de lijst met waarden onderaan het diagram.

In het geval van het Skew-T uit Donderdorp hebben we dus een potentiële CAPE van bijna 3100 J/kg. Dat biedt dus mogelijk garantie op zeer zware onweersbuien!

Let op: hier maken veel mensen tegelijk ook een fout. Een hoge CAPE zegt niets over de kans op onweersbuien. Het zegt enkel dat als er buien ontstaan, ze behoorlijk fel voor de dag kunnen komen. Het zegt dus iets over het onstabiliteits-ingrediënt, maar niets over de trigger!

Door naar de Lifted Index, die ook iets zegt over de onstabiliteit van de atmosfeer… 🙂

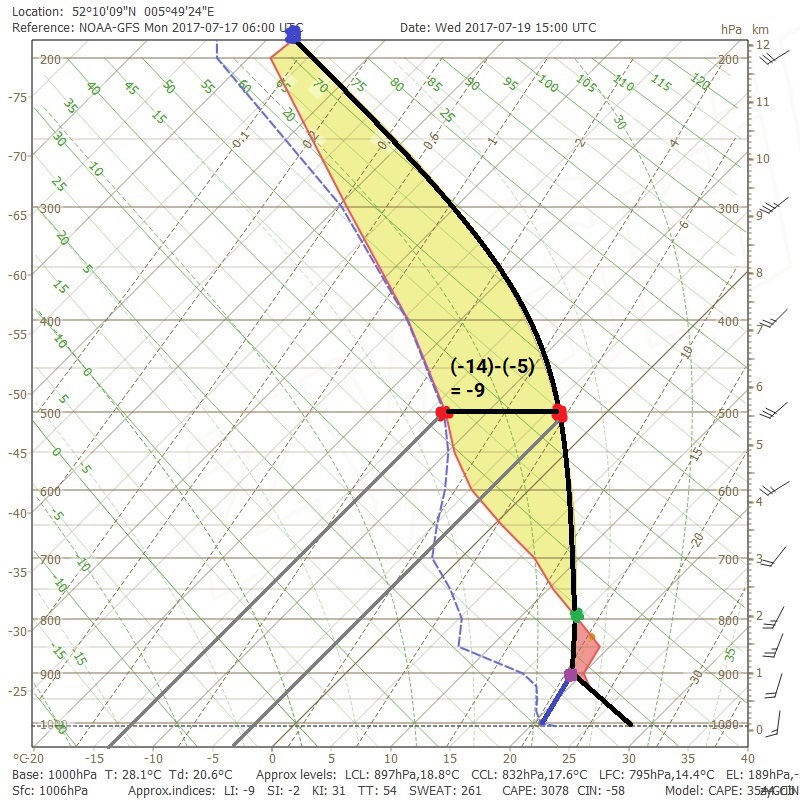Lifted Index

De Lifted Index is ook een veelgebruikte term binnen het verwachten van onweer. Bij deze index, die afgekort ook wel LI wordt genoemd, kijken we naar het verschil in temperatuur tussen de atmosfeer en een natadiabatisch stijgend deeltje op het 500 hPa-drukvlak.

Dat is een hoogte van circa 5,5 kilometer. Als een bui hier op zou houden, zou het geen zware bui worden.

Dus hoe groter het verschil is – mits de lucht koeler is dan het stijgende deeltje! – hoe kansrijker het is dat het luchtdeeltje nog veel verder stijgt.

De Lifted Index zegt dus niets over de kans op onweer, maar wel iets over de potentiële kracht van onweersbuien als een bui is ontstaan. Het is dus een maat voor onstabiliteit op hoogte.

Het bepalen van de Lixted Index gaat als volgt:

• Laat een deeltje adiabatisch stijgen tot 500 hPa (eerst droogadiabatisch, dan natadiabatisch);
• Bepaal middels de isothermen het verschil tussen temperatuur van atmosfeer en temperatuur van het deeltje.

Op het diagram is de atmosfeer circa -14 graden en het stijgende deeltje circa -5 graden. De Lifted Index is dan -9 graden (controle: ‘LI’ onderin het diagram).

Dat betekent dus dat als er buien ontstaan in Donderdorp, ze vanaf 5,5 kilometer nog een poosje door kunnen blijven groeien!

Voor onweersbuien in het zomerhalfjaar geldt dat een LI van ca. -5 voor felle buien kan zorgen, terwijl LI’s van -9 tot -11 kans op potentiëel zwaar onweer vertegenwoordigen.

Het ontstaan van bliksem

Er is sprake van ‘onweer’ als er een bliksemontlading plaatsvindt in de bui. En er zijn specifieke omstandigheden waaronder er in een bui bliksem kan optreden. Die zijn als volgt:

• Een redelijk sterke updraft en downdraft, eigenlijk altijd aanwezig in een bui;
• IJsdeeltjes!

Deze laatste zijn van groot belang bij het ontstaan van onweer. Doordat ijsdeeltjes op elkaar botsen, raken ze geladen (er vindt een zogeheten elektronensprong plaats tussen de deeltjes). De lichtere deeltjes, met een lading, worden met de updraft mee de hoogte ingevoerd, terwijl de wat zwaardere tegengestelde deeltjes blijven hangen. Het gevolg is dat er een spanningsverschil ontstaat in de bui dat moet worden opgelost…bliksem!

Tip 8: voor meer info over het ontstaan van bliksem, raden we ons artikel over elektrificatie van de bui aan.

IJsdeeltjes komen goed op gang vanaf circa -13 graden Celcius. Alles daarboven is ijs. Tussen 0 graden Celcius en -13 graden Celcius zien we onderkoelde waterdeeltjes – dus nog geen ijs – terwijl er steeds meer ijs begint te ontstaan.

Voor een onweersbui is het dus noodzakelijk dat een bui kan doorgroeien tot ‘boven’ het -13-graden-niveau. We kunnen het Skew-T-diagram gebruiken om te kijken of dat gebeurt.

Allereerst moeten we vinden op welke hoogte het adiabatisch stijgende deeltje het -13-graden-niveau tegenkomt.

We tekenen daarvoor in het Skew-T-diagram de -13-graden-isotherm.

Dat is de grijze lijn in het diagram.

We zien dat de CAPE (het gele deel) daar ver boven uitkomt. Het EL ligt zelfs helemaal bovenin het diagram.

Dat betekent maar één ding: zodra een deeltje boven het LFC uitkomt, kan het ver tot boven het -13-graden-niveau doorstijgen!

Meer dan de helft van de bui die over Donderdorp kan trekken lijkt dus uit ijs te bestaan. Bliksem kan zich vormen!

Als er een bui ontstaat, wat dan?

Dat is de volgende vraag die we moeten beantwoorden. We hebben inmiddels gekeken of er een bui kan ontstaan, en het antwoord is dat als er een voldoende grote trigger is, het tot zwaar onweer kan komen in Donderdorp. Maar hoe zwaar? En wat kan er dan precies gebeuren?

Er zijn verschillende parameters die op die vragen antwoord kunnen geven!

Die gaan we nu behandelen. We beginnen met het type bui, dat we bepalen op basis van het hodograph.

Het type bui – het hodograph

Aan de hand van het hodograph, waar we eerder over hebben gelezen, kunnen we bepalen wat voor type bui gaat ontstaan als het tot onweer komt!

Er zijn namelijk verschillende typen buien:

• Single cells: iedere bui is zijn eigen geïsoleerde losse ‘cel’;
• Multicells: de buien zijn met elkaar samengesmolten, vaak in de vorm van een buienlijn of -cluster. Kan gepaard gaan met zware weersverschijnselen!
• Supercell: de bui draait om zijn eigen as, waardoor het unieke karakteristieken gaat vertonen. Echte tornado’s (dus geen windhozen) zien we dan ook bij supercells ontstaan, net als enorme hagel.

Aan de hand van het hodograph kunnen we dus bepalen welk type cel het meest waarschijnlijk is.

Daarvoor moeten we eerst kijken naar de begrippen krimpende wind en ruimende wind.

Op het moment dat de windrichting verandert (of dat nu met de hoogte is of doordat de wind zelf verandert) kun je zeggen dat…

• De wind krimpend is als de windrichting tegen de richting van de klok in verandert;
• De wind ruimend is als de windrichting met de klok mee verandert.

De vereisten voor het type bui zijn als volgt:

• Voor een single cell:
  • Verandering in windrichting vindt niet plaats of is volstrekt ongeorganiseerd (dan weer dit, dan weer dat);
  • Weinig verandering in snelheid met de hoogte;
  • Winden in de bovenlucht zijn veel langzamer dan het geval is bij supercells.
• Voor een multicell:
  • Een licht ruimende wind met de hoogte tot ca. 300 hPa;
  • Daarna blijft de windrichting redelijk ‘gelijk’;
  • De windsnelheid neemt toe met de hoogte;
• Voor een supercell:
  • Een sterk ruimende wind tot ca. 300 hPa (d.w.z. een scherpe krul in de hodograph);
  • Ook nog wat ruiming boven 300 hPa;
  • Ca. 15 tot 20 kts windsnelheid onderin de atmosfeer en vanaf 300-500 hPa ~75-100 kts.
  • In de bovenste lagen van de atmosfeer windsnelheid zeer hoog.

Laten we die voor Donderdorp er nog even bij pakken:

Mijn conclusie is dat single tot ‘net’ multicells hier een realistische optie is.

Total Totals

Op het moment dat we weten dat er onweersbuien kunnen ontstaan moeten we een inschatting maken hoe zwaar ze kunnen worden. We hebben natuurlijk de ‘standaardwaarden’ zoals de CAPE en Lifted Index, maar in de loop der jaren zijn er meer parameters ontwikkeld.

De Total Totals (TT) index is daar één van. Het berekent als het ware de ‘kracht’ van onweersbuien vanaf de relatieve onderkant tot het midden van de atmosfeer.

De formule voor de TT is als volgt:

TT = (T850 – T500) + (Td850 – T500)

We kunnen aan de hand van de Skew-T bepalen wat de Total Totals is. Voor het Donderdorp-diagram doen we dat zo:

1. Op de 850 hPa-isobaar tekenen we een zwarte punt op het dauwpunt (Td850) en de temperatuurslijn (T850);
2. Op de 500 hPa-isobaar tekenen we een zwarte punt op de temperatuurslijn (500);
3. Met de isothermen bepalen we wat de temperaturen op die niveaus zijn:
   1. T500: -14
   2. Td850: +7
   3. T850: +19
4. We vullen deze waarden in de formule in en berekenen de Total Totals.

En voila, de berekening is voltooid!

Ter controle laten we in de afbeelding zien dat de berekening klopt met de automatische berekening onderin de Skew-T, rood omlijnd.

Maar wat doet de TT nu precies? Hij meet als het ware de som tussen het afnemen van de temperatuur en het dauwpunt. De betekenis van de Total Totals index is als volgt:

• Waarden onder 44: onweer is onwaarschijnlijk;
• 44 tot 50: onweer is mogelijk;
• 51-52: lokaal felle tot zware buien;
• 53-56: regionaal felle tot zware buien;
• >56: op gorte schaal zware buien mogelijk.

De Total Totals zegt weinig over de trigger, dus je kunt de index niet gebruiken los van de andere parameters en informatie die je onder andere van het Skew-T-diagram haalt.

K-Index

Net als de Total Totals is ook de K-Index (KI) een index om de kracht van onweersbuien te meten, op voorwaarde dat ze ontstaan. Hij zegt dus relatief weinig over een trigger, maar wel iets over de hoeveelheid onstabiliteit in de atmosfeer.

De K-index heeft een vergelijkbare formule:

KI = (T850 – T500) + (Td850 – Tdd700)

Let vooral op de dubbel-d bij het 700 hPa-drukvlak! We hebben het hier niet over het dauwpunt, maar over de dauwpuntsdepressie (die we eerder in dit artikel al dewpoint depression hebben genoemd).

De dewpoint depression is het verschil tussen temperatuur en dauwpunt op een bepaald drukvlak. In dit geval moeten we dus het drukvlak op 700 hPa nemen om de Tdd uit te rekenen.

Voor het Skew-T-diagram van Donderdorp gaat dat als volgt in zijn werk:

1. Op het 850 hPa-drukvlak tekenen we een zwarte stip op de dauwpuntslijn (Td850) en temperatuurslijn (T850);
2. Op het 700 hPa-drukvlak tekenen we een zwarte stip op de dauwpuntslijn (Td700) en temperatuurslijn (T700);
3. Op het 500 hPa-drukvlak tekenen we een zwarte stip op de temperatuurslijn (T500);
4. Met de isothermen kijken we naar de temperaturen voor iedere stip;
5. We berekenen de TDD700 als volgt: T700 – TD700;
6. Vervolgens vullen we de formule in voor de KI en krijgen we een getal.

En ook deze berekening hebben we succesvol afgerond 🙂

Voor Donderdorp komen we tot een K-Index van 31. Je kunt de waarde die je krijgt als volgt interpreteren:

• < 15: geen kans op onweer;
• 15-25: licht onweer mogelijk;
• 26-39: hier en daar fel onweer mogelijk;
• 40 of hoger: fel onweer mogelijk.

Hier en daar fel onweer dus, zo lijkt deze parameter uit te wijzen. Dat is behoorlijk in lijn met onze eerdere analyses! 😉

Wat we kunnen verwachten in Donderdorp

Op basis van het Skew-T-diagram voor Donderdorp kunnen we dus het volgende zeggen:

• Er is een lichte inversie (capping layer) die doorbroken zal moeten worden voordat luchtbellen vrij kunnen stijgen;
• Dat temperatuur dit doet is onwaarschijnlijk, dus zal een trigger in de vorm van lagedruk of bergen aanwezig moeten zijn;
• Zodra de luchtbellen wél boven het LFC kunnen uitstijgen, kan een bui doorgroeien tot 12 kilometer hoogte;
• Er is dus zwaar onweer mogelijk;
• Tegelijkertijd is er enige dynamiek aanwezig in de atmosfeer, waardoor we rekening moeten houden met geclusterde buien (in de vorm van een lijn of complex), hagel, windstoten, al kan het allemaal wat heftiger.

Stiekem was dit geen onweersituatie voor Donderdorp, maar de onweersituatie in Nederland van 19 juli 2017. Lees hier de verwachting én analyse waarom het uiteindelijk niet lukte met onweer:

• Spannende woensdag op komst: zwaar onweer mogelijk;
• Terugblik op 19 juli: wat ging er mis?

Conclusie

We hebben in dit artikel gezien wat Skew-T-diagrammen zijn, hoe je ze kunt interpreteren en belangrijker … hoe je ze kunt inzetten voor het maken van een onweersverwachting!

We hopen dat dit artikel informatief voor jullie is geweest 🙂

Wil je zelf een onweersverwachting maken? Gebruik dan de volgende checklist:

1. Bepaal de hoogtes van LCL en LFC. Wijken die af? Hoe sterk is een inversie?
2. Is er voldoende onstabiliteit (CAPE) aanwezig voor de vorming van onweersbuien?
3. Is de trigger sterk genoeg?
4. Kan bliksem ontstaan, dus groeit een stijgende bui door tot hoogtes boven het -13-graden-niveau?
5. Hoeveel dynamiek (schering) zit er in de atmosfeer en wat is het gevolg voor het type bui?

Succes! En onthoud: vragen mag je altijd stellen in de reactiebox hieronder 🙂

Bronnen

• KNMI: Weerballon of radiosonde;
• Skew-T log-P diagram;
• Skew-T info;
• Eigen kennis.